Тема уроку. Періодичність тригонометричних функцій. Графіки функцій у = sin х; у - cos x; y = tgx; y = ctg x .

Мета уроку: сформувати в учнів поняття про період і періодичні функції; ознайомити учнів із формулою для знаходження періоду функції виду у = f(kx + b); сформувати знан­ня формули періоду для тригонометричних функцій y = sinx, y = cosx, y~tgx, у = ctgx; сформувати вміння будувати графіки функцій у = sin х, у = cos х.

виховувати самостійність, акуратність при розрахунках;

розвивати логічне мислення.

Тип уроку: урок засвоєння нових знань і умінь

Методи навчання, прийоми: проблемно – пошуковий, наочний, бесіда, колективна робота, самостійна робота

Основні терміни і поняття: математична статистика, статистичне спостереження, вибірка, варіанта, варіаційний ряд, полігон, гістограма, середнє арифметичне, мода, медіана, розмах.

Міжпредметні зв’язки: __фізика – звукові й електромагнітні явища, біологія – серцева система, географія, астрономія - рух планет і т.д._______________________________________

Наочність: слайдова презентація

Технічні засоби навчання : мультимедійна система

План-конспект уроку

1. Організаційний етап

.

II. Актуалізація опорних знань учнів

Запитання до класу

1. Чому дорівнює sin 390°?

2. Чи правильно, що tg240° = √3 ?

3. Серед кутів 790°; 500°; -30°; -220°; -290° виберіть такі, внаслідок повороту на які початковий радіус буде розташова­ний так само, як і внаслідок повороту на 70°; 140°.

4. Пригадаємо, чому дорівнюють в радіанах кути:

0º, 30º, 60º, 90º, 120º, 150º, 180º, 270º, 360º (слайд 2)

III. Формулювання теми, мети й завдань уроку.
Мотивація навчальної діяльності учнів

У природі часто зустрічаються явища, які повторюються періодично. Наприклад, Земля в ході обертання навколо Сонця періодично повертається у своє початкове положення — через рік, два, три роки і т. д. Тому кажуть, що період обертання Землі навколо Сонця дорівнює одному року.

У техніці періодичний характер мають рухи колінчастого вала, маховика. У фізиці властивість періодичності мають звукові й електромагнітні явища. У біології періодичною є робота люд­ського серця.

Закономірності періодичних явищ описуються періодичними функціями, про які йтиметься на даному уроці.

IV. Формування нових знань (слайд3)

Пригадаємо, що спільного між кутами:...

Важливо!

Вся множина цих кутів записується так: , n Z де Z- множина цілих чисел

Зверніть увагу:

sin(-690º) = sin(-330º) = sin(30º) = sin(390º) = sin(750º) = sin(1140º)

cos(-690º) = cos(-330º) = cos(30º) = cos(390º) = cos(750º) = cos(1140º)

Учитель дає означення періодичної функції та показує (слайд 4), ви­користовуючи геометричну інтерпретацію, що sin(x + 2 n) = sinx і cos(x + 2 ) = cosx , ≠ 0 , n Z . Тобто довільне число 2 п , де п Z і п ≠ 0, є періодом для синуса й косинуса. (Т=2 ) — найменший додатний період цих функцій.

Використовуючи лінії тангенса й котангенса, неважко зробити

висновок, що tg(x + )=tgx i ctg(x + ) = ctgx .

Довільне число типу п , де neZ і п ≠ 0, є періодом тангенса й котангенса. Т = — найменший додатний період тангенса й ко­тангенса.

Учитель формулює твердження:

Якщо функція y=f{x) періодична і має період Т, то функція у = Af(kx + b), де A, k, b — сталі (к≠0), також є періодичною, причому їі період дорівнює

Правила знаходження періодів функцій (слайд 5) 

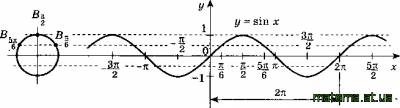
Графік функції y = sinx досить побудувати на відрізку [0;2 ] і з огляду на періодичність цієї функції продовжити його за допомогою паралельного перенесення побудованої частини на 2 , 4 , 6 , ... праворуч та ліворуч. У ході побудови скористаймося тим, що синус числа а — це ордината точки одиничного кола, у яку перехо­дить точка А (1; 0) внаслідок повороту навколо початку координат на а радіанів. Одержаний графік називають синусоїдою (рис. 1 і слайд 6).

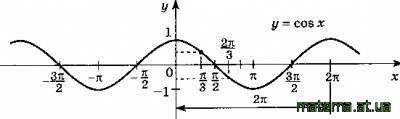
Графік функції y = cosx отримуємо із графіка функції y = sinx шляхом переміщення останнього вздовж осі Ох вліво на (слайд 7)

Примітка. Тригонометричні функції широко застосову­ють у математиці, фізиці й техніці. Наприклад, чимало проце­сів, як-от: коливання струни, маятника, напруга в колі змінного струму тощо — описуються функцією, що задається формулою у- A sin (сох+ ф). Такі процеси називають гармонічними коливан­нями. Графік функції у- A sin (сох+ ф) можна одержати із синусо­їди у = sinx стисненням або розтягненням її вздовж координатних осей і паралельним перенесенням уздовж осі Ох. Найчастіше гармо­нічне коливання є функцією часу t. Тоді воно задається формулою

y= A sin (ωx + φ), де А — амплітуда коливання, ω —частота, φ —

початкова фаза, — — період коливань.

V. Формування вмінь і відпрацьовування навичок Письмові вправи

1. Слайд 5. Вправи для самостійного виконання.

2. Обчисліть:

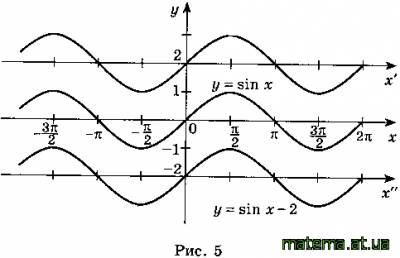
a)tgl860°; 6)ctgll25°; в) tg —; г) ctg —.

3. Знайдіть найменший додатний період функції:

а) у= sin4x; б) y = 3cos2x; в) у=5tg ( 5х +2); y = 0,3ctgl(0.3x + 1)

4. Побудуйте на одному рисунку графіки функцій: y = sinx , y = sinx + 2, y = sinx-2. Зазначте, за допомогою якого гео­метричного перетворення графіка y = sinx одержано графіки y= sinx + 2 і y = sinx-2 (Відповідь. Див. рис. ).

VI. Підбиття підсумків уроку.

Рефлексія

• Що ми вивчали сьогодні на уроці?

• Чи сподобався вам урок?

• Що вам більш за все сподобалось на уроці?

Запитання до класу

1. Укажіть, який найменший додатний період має кожна з функ­цій: y = sinx, y = cosx, y = tgx, y = ctgx .

2.  Яку функцію називають періодичною з періодом Т≠0?

3. Як використовують періодичність функцій для побудови гра­фіків?

VII. Домашнє завдання

Завантажити презентацію до уроку

http://matema.at.ua/periodichnist_trigonometrichnikh_funkcij.ppt